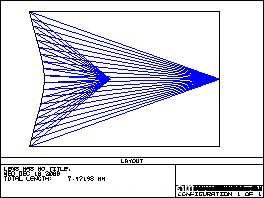
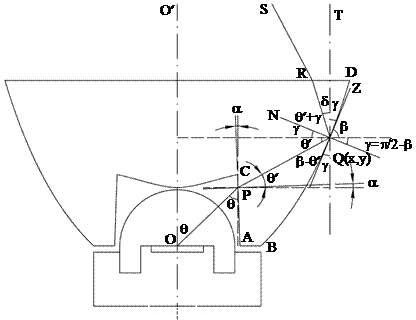
在透鏡的Y方向，內(nei) 凹的非球麵柱麵鏡的設計和外側(ce) 全反射麵輪廓線的設計如圖4的(a)和(b)所示。圖4(a)為(wei) Zemax中的光路圖，從(cong) LED射出的±40°以內(nei) 這部分光線，經過柱麵鏡折射之後，所有光線的反向延長線交於(yu) 虛焦點“F”，經過點“F”和柱麵鏡的邊緣所形成的邊緣光線，其與(yu) 光軸的夾角為(wei) ±19.6°，經過上表麵折射後，形成±30°的出射光線。圖4(b)為(wei) 用來計算外側(ce) 全反射輪廓線上各點坐標值的數學模型。其中q為(wei) LED出射光線OP與(yu) 光軸OO¢的夾角；Q(x,y)為(wei) 外側(ce) 全反射輪廓線上一點Q的坐標值，其反射線QR與(yu) 光軸的夾角為(wei) d；a為(wei) 全反射棱鏡入射麵的拔摸角，以利於(yu) 中間柱麵鏡模芯的拔出，這裏設置為(wei) 2°。

(a)

(b)

圖4(a)內(nei) 凹柱麵鏡Y方向剖麵在Zemax中的光路圖，(b)全反射棱鏡部分Y方向剖麵的數學建模

　　當q角從(cong) 90°變化到40°時，反射角d（即反射光線QR和豎直線QT之間的夾角）從(cong) 0°變化到19.6°。從(cong) 點Q(x,y)的角度關(guan) 係，可以得出以下的式子：

        (1)

        以及：

        (2)

        從(cong) 公式(1)及(2)，可得出以下的式子：

        (3)

　　其中，b為(wei) 曲線BD在點Q(x,y)處的切線角，g為(wei) 切線QZ與(yu) 豎線QT的夾角，PQ為(wei) P點位置的折射光線，q¢為(wei) PQ與(yu) 水平線之間的夾角。曲線BD的導數和切線角b的正切函數之間有如下的關(guan) 係：

        (4)

　　其中，dy和dx為(wei) 曲線BD在Y和X方向的微元。

根據在P點位置的斯涅爾定律[3][4]，有如下關(guan) 係：

　　因此：

        (5)

　　當q角從(cong) 90°變化到40°時，d從(cong) 0°漸變到19.6°，假設AB的初始值為(wei) 1mm，聯合公式(1)、(3)、(4)、和(5)，Q(x,y)點的坐標值可以通過數學模型的積分迭代法依次算出。

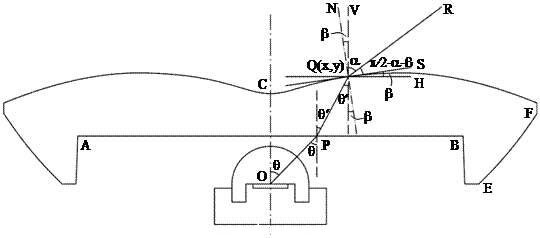
圖5：X剖麵，上表麵配光設計的數學模型

　　針對上表麵在X方向上的配光，其數學模型如圖5所示。根據柱麵鏡底部AB輪廓線上P點位置的斯涅爾定律，有

        (6)

　　再根據Q(x,y)點位置的斯涅爾定律，有如下關(guan) 係式：

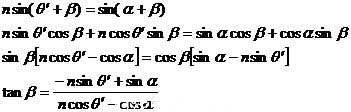        (7)

　　式中，a為(wei) 豎直線QV與(yu) 出射光線QR的夾角，b為(wei) 法線QN與(yu) 豎直線QV之間的夾角，q為(wei) LED的出射角，q¢為(wei) P點位置的折射角，n為(wei) 透鏡材料的折射率。為(wei) 了配成蝙蝠翼狀的光強的遠場角度分布，當LED的出射角q從(cong) 0°變化到76°時，輸出光線滿足以下的關(guan) 係：

        ,ifq£60°(8)

        以及

        ,if60

　　再根據以下曲線CF的微分和切線QS的正切角函數之間的關(guan) 係：

        (10)

　　聯合公式（6）至（10），上表麵的馬鞍形曲線CF的數值坐標可以用積分迭代法一一計算出來。