在工業(ye) 生產(chan) 中，常需要采用閉環控製方式來控製溫度、壓力、流量等連續變化的模擬量。無論是使用模擬控製器的模擬控製係統，還是使用計算機的數字控製係統，PID控製器都得到了廣泛的應用。這是因為(wei) 這種方法不需要精確的控製係統數學模型，有較強的靈活性和適應性。但是在數字PLC控製係統中，普通的 PID算法對所有過去狀態存在依賴性，從(cong) 而引起係統較大的超調，使係統穩定性下降。增量式PID控製算法每次輸出隻輸出控製增量，必要時可通過邏輯判斷限製故障時的輸出，從(cong) 而降低了因機器故障導致PID誤輸出給係統帶來嚴(yan) 重後果的影響。

　　在實際係統中，PLC控製模擬量可采用PLC自帶的PID過程控製模塊，但對要求比較高的場合采用改進的PID控製算法，就必須由用戶自己編製PID控製算法，基於(yu) 這些問題的考慮，文中介紹一種由三菱FX2N實現的增量式PID控製器的設計方法。

1 控製原理

　　1．1 PID控製原理

　　PLC的PID控製器的設計是以連續係統的PID控製規律為(wei) 基礎，將其數字化，寫(xie) 成離散形式的PID控製方程，再根據離散方程進行控製程序設計。

　　在連續係統中，典型的PID閉環控製係統如圖1所示，圖中sp(t)是給定值，pv(t)為(wei) 反饋量，c(t)為(wei) 係統的輸出量。

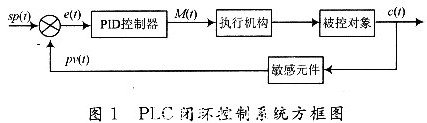
　　PID控製器的輸入／輸出關(guan) 係式為(wei) ：

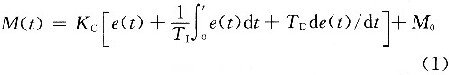
　　式中：M(t)為(wei) 控製器的輸出；M0為(wei) 輸出的初始值；e(t)=sp(t)-pv(t)為(wei) 誤差信號；Kc為(wei) 比例係數；T1為(wei) 積分時間常數；TD為(wei) 微分時間常數。

　　式(1)中等號右邊前3項分別是比例、積分、微分部分，他們(men) 分別與(yu) 誤差、誤差的積分和微分成正比。假設采樣周期為(wei) Ts，係統開始運行的時刻為(wei) t=0，用矩形積分來近似精確積分，用差分近似精確微分，將式(1)離散化，第n次采樣時控製器的輸出為(wei) ：

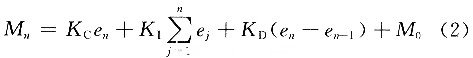
　　式中：en-1為(wei) 第n-1次采樣時的誤差值；K1為(wei) 積分係數；KD為(wei) 微分係數。

　　由式(2)可知，控製器輸出的第二項是誤差積累的結果，會(hui) 使得超調量過大，而這些在有些工業(ye) 過程中是不允許的。所以常規PID控製算法很難控製這類過程。

　　1．2 增量式PID控製規律

　　增量式PID的結構框圖如圖2所示：

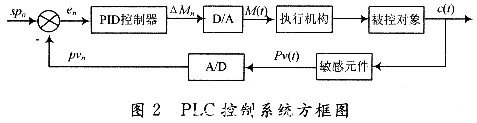
　　由式(2)的表達式，就可以根據“遞推原理”得到Mn-1的表達式：

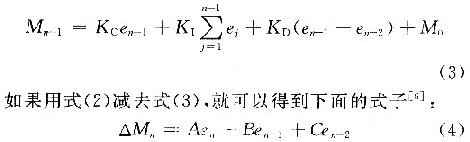
　　式中：A=KC+KI+KD；B=KC+2KD；C=KD。A，B，C都是與(yu) 采樣周期、比例係數、積分時間常數、微分時間常數有關(guan) 的常數。

　　由式(4)可知，增量式PID算法建立在對普通PID算法進行改進的基礎之上。它克服了位置式PID對所有過去狀態的依賴，計算機控製器輸出的隻是增量，所以誤動作的時候對輸出的影響比較小，必要的時候可以使用邏輯判斷的方法將這種影響消除，因而不會(hui) 嚴(yan) 重影響係統的工況。由於(yu) 算式中不需要對誤差進行累加，控製增量△Mn的確定僅(jin) 與(yu) 最近的n，n-1，n-2次的采樣值有關(guan) ，較容易的通過加權處理而獲得比較好的控製效果。

2 PLC軟件設計

　　2．1 程序流程

　　圖3給出了增量式PID控製算法的程序流程框圖。在進行初始化時，應根據係統性能要求選定參數KC，KI，KD和采樣時間TS，從(cong) 而確定係數A，B，C，並設置偏差初值en-1=en-2=0。

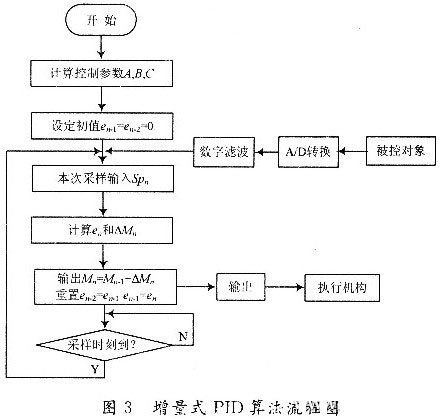
　　2．2 控製算法的參數確定

　　參數整定是控製係統設計的核心內(nei) 容。它是根據被控過程的特性確定PID控器的比例係數、積分時間和微分時間的大小，以改善係統的動態特性和靜態特性，取得最佳控製效果。本文采用臨(lin) 界比例度法。假設選取的控製度為(wei) 1．05，根據經驗選取臨(lin) 界比例度Kr=20％，臨(lin) 界振蕩周期Tr=60s，得參數整定初始值TS=O．90 s，KC=O．126，TI=30 s，TD=8 s。

　　基於(yu) 三菱FX2NPLC的部分程序如下：

　　
3 結語

　　該文在分析普通PID控製算法的基礎上，提出了增量式PID算法的控製原理，通過了自編程序在三菱FX2NPLC上實現了改進的PID算法。由實際模型的驗證結果表明，此方法可以有效地減少係統的超調量，使其得到更好的控製效果，因此在實際的工程應用中具有較好的借鑒作用。